Математики уже давно научились меряться у кого бесконечность больше. И если конкретно, то это началось с одного математика Георга Кантора создавшего
теорию множеств. Он доказал существование иерархии бесконечностей, каждая из которых больше предшествующей. Его теория множеств один из краеугольных камней математики.
Начала теории множеств по идее должны изучать в школе. Ну там, множества состоят из элементов, они могут объединятся, пересекаться, есть конечные и бесконечные множества и тд. Поэтому в подробности тут я вдаваться не буду.
Абстрактно, множество это совокупность его элементов. Конченые множества к примеру можно представить так {1,2,3,4}, {0,1,3,4,8,10,14} или {a,b,c} и тому подобное.
Бесконечные множества это к примеру множество всех натуральных чисел {1,2,3,4... и т.д.}, четных {2,4,6,8... и т.д.}, нечетных, рациональных, вещественных и много других.
Множества можно сравнивать по количеству их элементов, что будет являться их мощностью (
кардинальным числом). С кончеными множествами все просто сколько элементов внутри, такова их мощность. Мощности множеств равны если их кардинальные числа совпадают. Это еще можно определить через взаимно-однозначное соответствие разбив их на пары. Вот к пример множества A{1,7,3,5} и B{a,b,c,d}.
A 1 7 3 5
B a b c d
каждой твари по паре и поэтому эти множества равны. А их кардинальное число равно четырем.
Но что насчет бесконечных множеств? Какова мощность множества натуральных чисел? Мощность есть и кардинальное число здесь будет равно алеф-нуль, что означает бесконечность счетных чисел. Но как же мощность множества четных чисел? Их же должно быть меньше чем натуральных? Нет, вспомним взаимно-однозначное соответствие.
M 1 2 3 4 5 ...
N 2 4 6 8 10 ...
Мощности их равны алеф-нуль
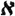 0
0. Тоже самое будет с нечетными, или рациональными или к примеру с целыми

Все бесконечные множества которые можно посчитать натуральными числами называются счетными.
Тут возникает забавное отличие между конченым и бесконечным. Если мощность суммы конечных множеств будет больше чем мощность каждого отдельного множества. То у бесконечных счетных оно не меняется. Бесконечность плюс бесконечность равно бесконечность и эти бесконечности равны. Прежде чем идти дальше и более подробно разобрать понятие кардинального числа, нужно разобраться с такой вещью как
ординальное число(порядковое число).
Грубо говоря ординалами нумеруют порядок элементов. Возьмем тоже конечное множество A{1,7,3,5} и пронумеруем по порядку его элементы.
1 7 3 5
1 2 3 4
Как можно заметить самый большой ординал в этом множестве равен кардинальному числу этого множества и вполне себе очевидно, что в любом конечном множестве наибольший ординал и кардинальное число равны. Ну что случится если мы перейдем к бесконечным множествам? Возьмем множество натуральных чисел {1, 2, 3, 4, 5, 6 и т.д} если мы все эти элементы пронумеруем, то каким будет его наибольший ординал? Тут вводится наименьшее бесконечно большое число ω (омега) и тут начинается царство трансфинитных чисел. Начиная с ω мы можем дальше делать трансфинитные числа ω+1, ω+2, ω+ω что эквивалентно 2ω, а также ω2 или ω
ω и так далее. Но что же получается, значит ли это, что ω+1 больше ω которая является бесконечно большим числом? Нет, еще раз, ординалы служат инструментом упорядочивания, а не обозначения размера. Если мы возьмем тоже множество натуральных чисел, но только решим в начале пронумеровать четные, а затем нечетные, то заметим для нумеровки всех четных чисел на понадобятся все ординалы вплоть до ω, но нам нужно пронумеровать еще и нечетные, тут и понадобятся трансфинитные ω+1, ω+2 вплоть до 2ω. А так как я ранее уже показал, что множества натуральных, четных и нечетных равны по мощности, то и трансфинитные числа в первую очередь говорят не о размере, а лишь о порядке. Размер же их будет обозначатся кардинальным числом алеф-нуль. Можно лишь сказать, что когда множество имеет ординал с ω, то она становится бесконечным множеством мощности алеф-нуль, но если имеется ω+1, то это не говорит о большей мощности, а лишь о другом порядке нумерации (к примеру если начал считать натуральные числа с двойки, а не с единицы, а саму единицу присобачил после бесконечности натуральных чисел). Ладно, об ординалах поговорили, но мы к ним еще вернемся. А пока зададимся другим вопросом. Есть ли бесконечность, которая имеет большее кардинальное число чем алеф-нуль? Есть ли бесконечное множество которое в буквальном смысле содержит больше чисел чем множество натуральных чисел?
Есть, и это вещественные (действительные) числа. То есть множество которое кроме рациональных чисел содержит и иррациональные, такие как Пи, е логарифма, корень из двух, короче любая десятичная бесконечная не повторяющаяся дробь.
Для того что бы это понять, давайте попробуем провести взаимно-однозначное соответствие натуральных и вещественных чисел.

Жирным выделены диагональю 1, 4, 1, 0, 0, 3, 1, 4, 8, 5, 1... Теперь сделаем такой алгоритм создающий еще одно действительное число, если цифра на диагонали равна 1, то цифра разряда создаваемого числа будет равна 3 и если не равна, то 2, тогда мы получим число: 0,32322232223...
У этого числа не будет взаимного-соответствия с множеством натуральных чисел, так как все действительные числа к кому были подставлены натуральные имеют различия хотя бы в одном разряде. А так как таких алгоритмов мы можем придумать бесконечно много, становится очевидным, что бесконечность натуральных чисел меньше бесконечности вещественных. Причем неизмеримо, в интервале от 0 до 1 вещественных чисел будет больше чем бесконечности натуральных и в интервале от 0 до 0.5 и в интервале от 0 до 0.1 и т.д. Вот насколько крута мощность вещественных чисел, кардинальное число здесь называется континуумом.
А что насчет других кардиналов больше алеф-нуль? Есть такие, булиан от алеф-нуля. И если отвечать на вопрос, что такое булиан, то это множество из всех подмножеств множества. Вернемся к конечным множеством, из множества {1,2,3} мощность три, можно сделать множество из всех его подмножеств {{},{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3}} мощность 8 ({} это пустое множество и это отдельный разговор). И это же справедливо для бесконечных натуральных множеств, их булиан будет равен мощности алеф-один
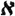 1
1, а булиан алеф-один это алеф-два
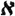 2
2 и т.д. Или если мы опять вернемся к ординалам, возьмем последовательность множество всех ординалов счетных множеств

И когда я говорю все, я имею ввиду всю эту бесконечную трансфинитную наращиваемость, то это множество образует первое несчетное порядковое число ω
1, соответствующее кардинальному числу алеф-один. Таким же образом мы можем получить ω
2 и алеф-два. Ну и так далее и так далее. В итоге мы получаем иерархию все больших бесконечностей, где каждая бесконечность в буквальном смысле больше прошлой, причем настолько больше, что прошлая бесконечность внутри нее ничтожна, что ее мера равна нулю (меры множеств это отдельный, но тоже интересный разговор). Это иерархия является
иерархией алефов. Причем заметим насчет индексов этих алефов. Ими могут быть трансфинитные ω (омега). Алеф-омега это самый маленький несчетный сингулярный кардинал. И мы можем взять Алеф-ω
1 и Алеф-ω
ω и дальше. Процессу ничто не мешает, даже если мы просто потеряем возможность записывать этот индекс, потому что не придумали еще способ записи.
(Кстати, если вы спросите где среди этих алефов будет континуум, то это неизвестно. Гипотеза о том, что континуум равен алеф-один называется континуум-гипотезой и она до сих пор не доказана.)
Вы можете спросить, а есть ли что-то за пределами этого? За пределами всей этой беспредельной иерархии алефов? С некоторыми нюансами, но есть. Входной точкой будет так называемый недостижимый кардинал и тут бесконечные множества становятся действительно большими.

























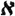 0. Тоже самое будет с нечетными, или рациональными или к примеру с целыми
0. Тоже самое будет с нечетными, или рациональными или к примеру с целыми


